May the funny Christmas be with you

突然ですがこの↑ヘッダーと言うんでしょうか、この上の緑色とか肌色のやつ、ボロノイ図っぽいですよね(ボロノイ図 - Wikipedia)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


さて、読者の厳選も済んだことですし始めていきましょう、

 

 

 

 

 

 

 

 

 

こんにちはこんばんは皆さん、クリスマスどうお過ごしでしょうか、この記事は図らずもMice Advent Calendar 2018 - Adventarのラストを、そう、12月25日を飾ってしまう事になった悲しいブログです。

 

皆さま、今晩、このクリスマス夜、何が起こるか分かりません、右手にパンの切れ端、左手にぶどう酒でも用意して、不穏な位置情報を見せる友人やtwitterの更新の減った知人、信じていたはずの隣人に即座に渡せるようにしてからお読みください。(未成年の方はファンタグレープでも良いと思います)

 

 

 

 

 

「主よ、それは誰のことですか」

 

 「わたしがパン切れを浸して与えるのがその人だ」

  

　(ヨハネ13:23-26,新共同訳)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

はい、では綴っていこうと思います。

 

 

まぁまず、そうですね、見てください↓この↓並び

f:id:heuu:20181224035042p:plain

2017年アドベントカレンダーより

f:id:heuu:20181224035117p:plain

2018年アドベントカレンダーより

 この前々副部長のお二方、文才もありますし、書いてる内容もなかなか良いのでこの並びプレッシャー凄いんですよね。

 今年の彼らの記事は、たっぺー君が順調なアル中街道のまっしぐらな記事で、ぬぬぬはバックアップの話でしたね。(そして最後に締めくくれとくぎさされてましたね..がんばる) 

 

 

 

 いや、そんなことはどうだっていいんです、そう、もっと言いたいことがあります、なぜ私なのか、この日にブログを書くのにもっと適した人がいたのではないか、そう私は感じてはいます、(まぁ自分で選んだんですが)

 

 

 

 

 

 

 

 

 

 

が、どうにかこうにか言葉を紡いで行こうと思います、頑張ります。

 

 

 

 

 

 

 


まずここまでアドベントカレンダーでブログを書いて来た皆さん、お疲れ様です、そしてこのアドベントカレンダーをやりだした後輩の勇気を讃えたいと思います、来年も日本が存在していたらやりましょ。(いやそこはあんまり関係ないですね)

 

 

 

 

 

 

 

 


しかし、一方で、まぁ、よくも巻き込んでくれましたね、
ステルス決め込んでみんなのブログゆっくり見ようかなぁと思ってたら書く側になっちゃいましたよ、ハハハ…(・∀・)

 

ありがたがるべきなのですかね？

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


まぁいいです、アドベントカレンダー最終日ですし、そんな後輩の初日のブログの答え合わせをしておきましょう

 

 

 


皆さんアドベントカレンダー初日のブログは読みましたか？(まだ読んでない方は読んできましょう→Nemuineko)

 

 


最後まで読むと何やら意味深なことが書いてありましたね

その答え合わせをしておきましょう

 

以下答えとなっております(雑な)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

答えは

  • 「今日から25日間」では無いですね、24日間ですね。
  • 書いた本が違いますね。(すいません各自調べてください)
  • 歳が37ではない、算数の話ですね、ちゃんと足してみよう。

 らしいです。

 

 

 

 

 

 

 

 

 

 

みんなは〜〜いくつ～～あってた〜〜？？？？？？？

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 まぁみんなが答えを分かったところでこの記事の本題に入って行きたいと思います。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

f:id:heuu:20181222052838p:plain

ててててーん～てーん～ててててーんてん～ててててーんてん～てててて～～



 

 

 

 

 

 

 

 

 

 

算数の話 (小難しい話が苦手な人は振り返りまで飛ばしてください)

 

 

皆さまは、「変分法」ってご存知ですか？又の名を「汎関数微分法」などとも言うようです、聞いたことなど御座いますでしょうか？

 

 

 

 

そこはかとなく想像はしておりましたが全微分にピークが出来てますね、まぁ全微分までは結構大学(教育機関)でも丁寧に教えてくれる気がするので納得といえば納得の結果です。

 

 

 

 

 

 

 

 

 

 

変分法とは
「解析学の一分野、変分法（へんぶんほう、英: calculus of variations, variational calculus; 変分解析学）は、汎函数（函数の集合から実数への写像）の最大化や最小化を扱う。汎函数はしばしば函数とその導函数を含む定積分として表される。この分野の主な興味の対象は、与えられた汎函数を最大・最小とするような「極値」函数、あるいは汎函数の変化率を零とする「停留」函数である。(wikipediaより)(ありがとう)」です。

 

 

 

 

なるほど†完璧†に理解しましたね。日本人なので日本語で書いてある文書を難なく†完璧†に読めました。日本語さいこー日本語ありがとうー

 

 

 

 

 

 

 

 

 

 

 

まぁ、今のwikiコピペで理解できた人はいい感じに流し読みして行ってください

少なくとも私は「汎」とか「函」とか若干怪しかったです、悲しいね。因みに「はん」「かん」です。

 

 

 

 

 

 

 

 


ここから半ば自分の備忘録として変分、変分法について振り返って行こうと思います。分かっている方も多いと思うので復習がてらさらさらと見て行ってください。(至らない点等多々あると思いますがクリスマスですし大目に見ていただけると助かります。)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

早速ですが、変分は雰囲気は微分と同じです。

 


これだけ聞いても何を言ってるんだ？って感じだと思うので微分あたりから(可能な限り)丁寧に振り返ってみます。

 

 


という事で一先ず微分の振り返りから行きますね。

 

 

ある関数 { \displaystyle \textit{y} } が { \displaystyle \textit{x} } によって値が一つに定まるとします。{ \displaystyle \textit{y} }({ \displaystyle \textit{x} }) こう書けますね。つまるところ、よく聞く普通の関数を { \displaystyle \textit{y} }({ \displaystyle \textit{x} })って書くよって言うだけです。

 

この時ある適当な距離{ \displaystyle \textit{h} }だけ{ \displaystyle \textit{x} }が増えたとします。

そして今、{ \displaystyle \textit{x} } が { \displaystyle \textit{h} } だけ増えたらどれくらい { \displaystyle \textit{y}} が増えるのか知りたいとしましょう。

下の図１- (a)のような状態ですね。繰り返しになりますがこの青い線の傾きがいま我々が求めたいものです。

f:id:heuu:20181223004917p:plain

図１微分の図



 

 

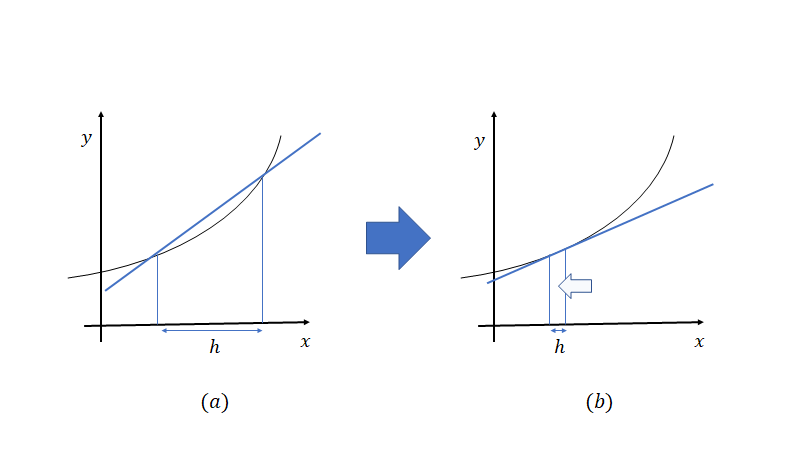
そしてこの { \displaystyle \textit{h} } の大きさを小さくしていきます。すると上の図1- (b)のようになって行きますね。このまま { \displaystyle \textit{h} } を限りなく0に近づけていくと、ある { \displaystyle \textit{x} } での傾きが分かることになります。

 そしてこれを以下のように書くわけです。

 

\begin{equation}\frac{dy}{dx} = \lim_{h \to 0}\frac{y(x+h)-y(x)}{h} \end{equation}

 

 この値を { \displaystyle \textit{f'} }({ \displaystyle \textit{x} }) と書いたりするわけですね。これが良き聞く微分ですね、この定義を毎回  sin({ \displaystyle \textit{x} }) や exp({ \displaystyle \textit{x} }) にいれてやり極限の計算をしてやればよいですがまぁ大体公式で覚えていますよね。少なくと私にとっては道具なので普段はそこまで深く考えていませんが、たまに定義に振り替えることもあります。

 

 またこの時、本当は微分可能とか右側極限と左側極限が同じ値になるかなど確かめなければならないことや、より広い定義の弱微分、劣微分、フレシェ微分などいろいろありますが、それは興味の出た皆さんで各自調べて行ってください

 

 

 

 

 


次に偏微分です。

 読んで字のごとく偏った微分です、なにに偏るのかと言うと { \displaystyle \textit{x} } 軸や { \displaystyle \textit{y} } 軸など特定の軸方向だけのことを考えて微分するわけです。以下図を見つつさらさらと説明して行きます。

 

f:id:heuu:20181222053417p:plain

図２偏微分の図


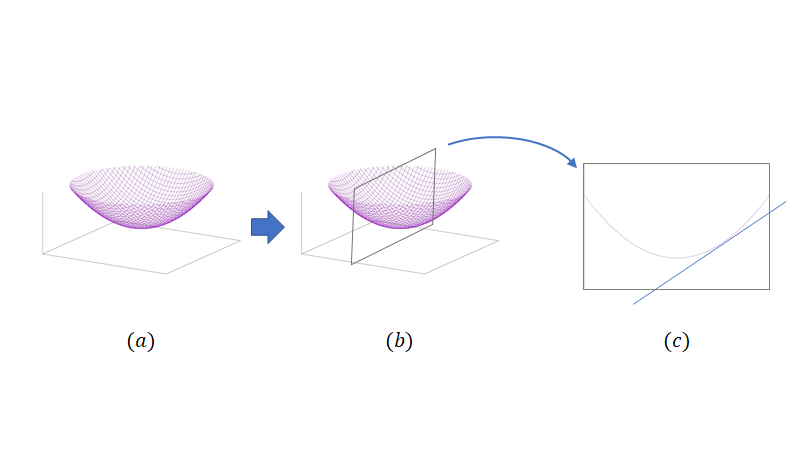
図２-(a)のお椀のような図形を考えます、そして図２-(b)のように特定の軸方向だけ切り出してきます。そして図２-(c)のようにその面で微分してあげればよいのです。この時関数に他の軸の情報は定数として扱います。例えば { \displaystyle \textit{x} } 方向に偏微分している場合は { \displaystyle \textit{y} } は定数として扱ってよいという感じです。

表式としては 

\begin{equation}\frac{\partial z}{\partial x} \end{equation}

 のように書きます。{ \displaystyle \partial}はパーシャルまたはラウンドと読みます。

 

 

 まあ断面を見ていけばいいんですね。

次元を落として考えて行きましょう。お世話になった塾講の先生も言ってました、「我々には三次元は早い」と(蛇足ですね)

 

 

 

 

そして全微分ですね、今三次元図３-(a)のようにある関数 { \displaystyle \textit{z} }({ \displaystyle \textit{x} } , { \displaystyle \textit{y} }) があるとします。 { \displaystyle \textit{x} }, { \displaystyle \textit{y} } によって { \displaystyle \textit{z} } の値が変化するような状態を考えます。 

 このとき { \displaystyle \textit{z} } の変化分を { \displaystyle \textit{dz} } とすると

 \begin{eqnarray} dz&=&z(x+dx, y+dy) -z(x, y)\\ &=&z(x+dx, y+dy) -z(x+dx, y)+z(x+dx, y)-z(x, y)\\&=& z(x+dx, y+dy)-z(x+dx, y) \\&\quad&+z(x+dx, y)-z(x, y) \end{eqnarray} 

と言うように式変形できます。

また最終行の式については図３-(b)の黄色と青の直角三角形の最短辺についてたし合わせていることになりますね。 

f:id:heuu:20181222053512p:plain

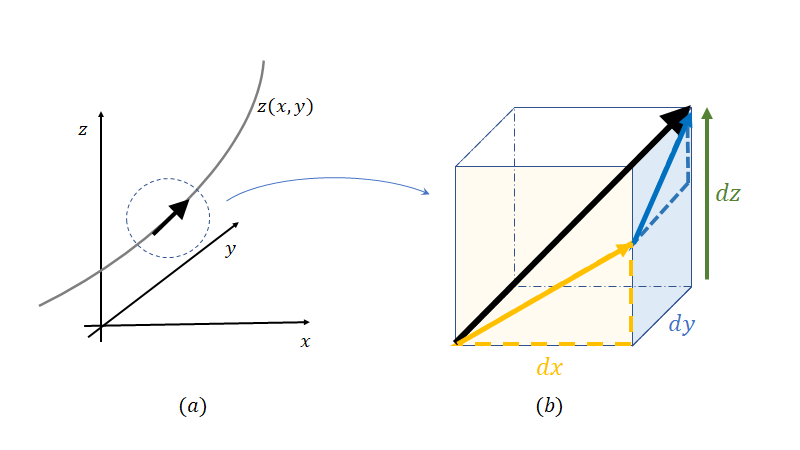
 ここで { \displaystyle \textit{dx} } が微少量であることを考えると

 \begin{eqnarray}  z(x+dx, y+dy)-z(x+dx, y) \simeq z(x, y+dy)-z(x, y)\end{eqnarray}

 と考えることが出来ます。すると

 \begin{eqnarray}  \lim_{y \to 0 }(z(x, y+dy)-z(x, y)) = \lim_{y \to 0}\frac{z(x, y+dy)-z(x, y)}{dy}dy =\frac{\partial z}{\partial y}dy\end{eqnarray}

 \begin{eqnarray}  \lim_{x \to 0 }(z(x+dx, y)-z(x, y)) = \lim_{dx \to 0}\frac{z(x+dx, y)-z(x, y)}{dx}dx =\frac{\partial z}{\partial x}dx\end{eqnarray}

 

よって

\begin{eqnarray} dz=\frac{\partial z}{\partial y}dy+\frac{\partial z}{\partial x}dx \end{eqnarray}

となるわけです、イメージとしては { \displaystyle \textit{x} } , { \displaystyle \textit{y} }方向にそれぞれどれだけ増加するかを調べてあげて、微少量かけてあげた感じですね。よかったよかった。 

 

 

 

 

 

 

 

 

さていよいよ本題の変分に入ります。

まず変分の事を説明の都合上、汎関数微分と呼んで進めていきます。意味は全く一緒です。(違っていたらすみません)

 

ということで変分とは汎関数を微分すればよいことが分かりました。

 

 では次に汎関数とは何なのか考えましょう。

 

関数の変数が関数であるようなものを汎関数というのですが、これだけ聞くと合成関数のようなものをイメージすると思います。↓こんなのですね

\begin{eqnarray} f(g(x))=g^2(x)+\sin(g(x)) \end{eqnarray}

これはある { \displaystyle \textit{x} } の値で { \displaystyle \textit{f} } が決まると言う事ですね。汎関数はこうではありません、ある「関数」が決まると関数の値が決定されるのです。

 

\begin{eqnarray} f[g(x)]=\int_{A}^{B} g(x)dx\end{eqnarray}

これなら { \displaystyle \textit{x} } の値ではなく関数の形で { \displaystyle \textit{f} } の値が決まりますね。これが汎関数です。

 

そしてこれを微分するわけです。

 

そもそも微分とは変数を微少量変化させたときに関数がどれほど変わるか知りたいというものでした。

 

汎関数微分は、関数を微少量変化させたとき、もとの関数がどれだけ変化するかを知りたいというものです。 これを念頭に以下の式を見ていきましょう。

 

\begin{eqnarray} \delta f[g(x)]&=&\int_{A}^{B} \{g(x)+\delta g(x) \}dx-\int_{A}^{B} {g(x) }dx&=& \int_{A}^{B} \delta g(x)dx\end{eqnarray}

 

ここで

\begin{eqnarray}g(x, y, z)=g(x, y(x), \frac{\partial y}{\partial x}) \end{eqnarray}

であるとすると

\begin{eqnarray}\delta g=\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial z}\delta z =\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial (\frac{\partial y}{\partial x})}\delta (\frac{\partial y}{\partial x}) \end{eqnarray}

となりますね。 

 

よって汎関数は

\begin{eqnarray} \delta f[g(x)]=\int_{A}^{B} \{\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial (\frac{\partial y}{\partial x})}\delta (\frac{\partial y}{\partial x}) \}dx\end{eqnarray}

となります。

ここで第二項を部分積分して { \displaystyle \delta}{ \displaystyle \textit{y} } を括りだすことを念頭において式計算していきます。また { \displaystyle \delta }{ \displaystyle \textit{y} }({ \displaystyle \textit{A} })={ \displaystyle \delta }{ \displaystyle \textit{y} }({ \displaystyle \textit{B} })=0であるとします。すると

\begin{eqnarray}\int_{A}^{B}\frac{\partial g}{\partial (\frac{dy}{dx})}\frac{d(\delta y)}{dx}dx&=&\left[\frac{\partial g}{\partial (\frac{dy}{dx})}\delta y \right ]_{A}^{B} -\int_{A}^{B}\left[\frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \right ] \delta y dx &=&-\int_{A}^{B}\left[\frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \right ] \delta y dx\end{eqnarray}

 となります

 そして元の式に戻してあげると

\begin{eqnarray}  \delta f[g(x)]=\int_{A}^{B} \{\frac{\partial g}{fpartial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})}\} \delta y dx\end{eqnarray}

 

式変形し 

\begin{eqnarray}  \delta f[g(x)]&=&\int_{A}^{B} \{\frac{\partial g}{\partial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})}\} \delta y dx&=&\int_{A}^{B}G(x)\delta y(x)dx\end{eqnarray}

 

ここで 

\begin{eqnarray} G(x)=\frac{ \delta f}{\delta y }=\frac{\partial g}{\partial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \end{eqnarray}

とし、これが汎関数微分です。やりましたね。

関数で関数を微分したような形になってますね。

そしてここからが本題です。微分と同様にこの汎関数微分が0になるところを調べてあげることで変化率がゼロの点の集合、つまり図４のように谷の一番深いところ、水が流れていく川の形が関数として分かると言う事なのです。

f:id:heuu:20181224185524p:plain

図４

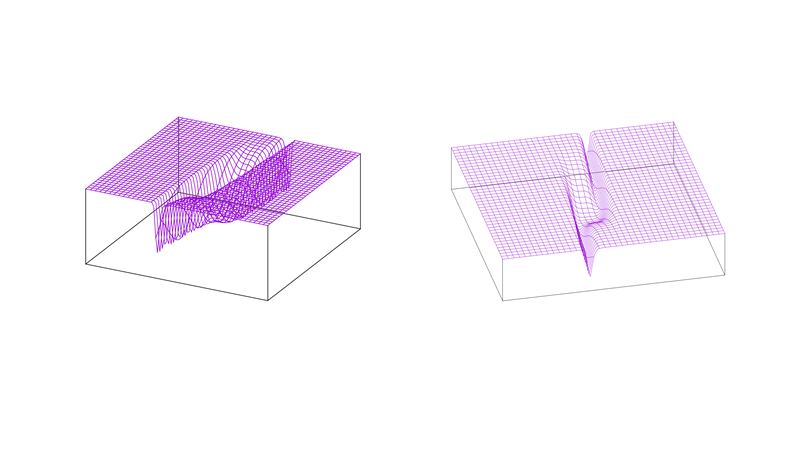
これはオイラー・ラグランジュ方程式を解くことと同義であるわけで、最後にやることとしては、オイラー・ラグランジュ方程式を解く事で光路や電線の垂れた形の関数、最速降下線などを求めることが出来るのですね、大切ですね。やったね。

 

ここからはマウサーに送る言葉です、これを使ってターン起動とか求めたら良さそうですよね、誰かやってみてください。

 

 

 

 

 

ふぅ、ちょっと尻すぼみになってしまいましたが疲れてしまったので勘弁してください、もし気が向いたらまたの機会により詳しく書こうと思います。気が向いたらね…

 

 

 

 振り返り

 

さて算数の話はここまでにして、ここからは今年の振り返ってみたいと思います。

 

今年は災害も多く、私のマウスもなかなか動かず、年号もなかなか発表されず、良く分からないゴタゴタカナワゲートウェイなど良く分からない問題が間々あり、大変な一年でしたね。

皆さんの周りはそうでしたか？マウスははしりましたか？やりたかったことはできましたか？

 

 

 

しかし一方で良いこともありました、RTが唐揚げロボットで世間から注目されたり、RTが技術業績賞を取ったり、オモシロ醜態動画が撮れたり、大阪万博が決まったり(ん??)、夏休みにふらふら学生気分で旅をして楽しかったり( 夏に宿を貸していただいた先輩方並びに他大学の方ありがとうございました)、位置情報が流行ったり、彼女が出来たり、結婚したり、新しい猫さんが家に来たり、私にも皆さんにも良いことがたくさんあったように思います。

 

 

新しい世代の猫さんです↓

f:id:heuu:20181224033518j:plain

左「ぼっちゃん」右「おじょーさん」父命名



 

可愛らしい↓

f:id:heuu:20181224033731j:plain

kawaii

 

 かわいいですね。まちがいない。

 

 

 

 

 そして今年の私風呂事情です↓

  •  ボディーソープはバウンシアのこれ→(Amazon CAPTCHA )
  • シャンプーはボタニカル系のやつらです(各々調べてください)(いいのあったら教えてください)
  •  リンスはボタニストのしゅっしゅするやつです→ (Amazon CAPTCHA)

 

このリンスがですね、最高なんですよ、私は普段リンスなんてつけない人なんですがこればかりはつけてます、最高です。最高ですよ！！！

 

 

 

 

 

 

 

 

 

最高ですよ！！！！

 

 

 

 

 

 

 

 

 

そして今年はまったものです↓

 

ちぃたんと言うコツメカワウソ、ポップティーン専属モデル、秋葉原観光推進協会、高知県観光大使などの属性をもつゆるキャラです。

 

お気に入りの動画です↓ 

 

 

あとパンダの着ぐるみに押し倒されるのとかも好きです、良かったら探してみてください。 

 

 

 

 

 

 

 

 

 

 

そしてこれはちょっとした恒例のライフハック情報です、

お食事処等(見栄えのいい)の検索術するとき、インスタでハッシュタグ検索するといい感じの写真とともに、お店が見つかるようです。大切な人や見栄を張りたいときに使えます。これを機に皆さんもインスタ始めて見てはいかがでしょう？

 

 

 

 

 

 

 

 

 

 

そして以下、とある筋から入手したイシカワ調べの今年のJKトレンドです。

 

  • ゼペット
    アイコンを作ったり、"写真の盛る"の"そのさらに先"のような使い方をする様です、アバターを作って可愛い自分を演出するらしいです。興味あるかたインスタとかで検索かけてみてください。(ゼペット用のインスタのアカウントとか作っている人もいるようです、文化って面白いですね)
  • ゼンディ
    JK版位置情報共有ですね、今や「なんでこの子の連絡先持ってるの！？」から「なんでこの子の位置情報持ってるの！？」で破局する時代らしいです。高度な情報戦が繰り広げられていそうですね、どきどきしますね。SNSのその先のような感じなのでしょうか？(ま.ぁ位置情報、たのしいですよね)
  • ピンクピンクモンスター
    モンスター級にもれるプリクラ機らしいです、今トレンドは透け感とかで、なんかすごいらしいです。さらに最近のプリ機はスイカとか電子マネーで行けるらしいです。しっかり時代についてきてますね。(すみません私には良く分かりません)
  • デイリージェニック
    インスタ映えは一周してダサいらしい、普段の一場面を切り取ったように盛ったようなものを写真でSNSなどに上げるらしいです。(ミスコンの写真などもそんな感じでしたね)

 

以上が大まかに調べて分かったことです。「盛りすぎない」「シンプル」「自然体」などがトレンドの様です。

 

昔は「若者の文化」などと自分たちの行動に名前を付けられていることに対して不思議な感覚がありましたが、年齢を重ねてみると頷けるものがあります、時代の流れに既に取り残されているのでしょうか。

 

 

はぁ、もうおじさんなんですね、歳、とってしまいましたね。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 さて来年はどんな年になるのでしょうか(年号的にも)

 

 

 

 私は出来ればたくさんの大会でいろんな人とお話しして新しいことを発見できたらいいなーとか、楽しい研究がこのまま出来たらなーとか思ってます。

 

 

 

 

 

 そして良ければみなさん年賀状を下さい、送ってくださる方はtwitterなどで話しかけてください！お待ちしております！

  

 

 では皆さん残り少ない平成を陽気にお過ごしください。

 

 

 

 

 

 

 あ、最後に一つだけ、

 

 積分にも微分→変分の様な関係性のものが存在します
経路積分、汎関数積分という様な名前が付いています

ほぅ...なるほどねぇ…

 

 

 

 

 

 

 

 

 

 


ところでこいつをみてくれ！！↓

 

f:id:heuu:20181224042502g:plain

電子のg因子に寄与する光子5個を含むファインマン図の代表例

物理学史上、最も精密な理論計算値 | 理化学研究所


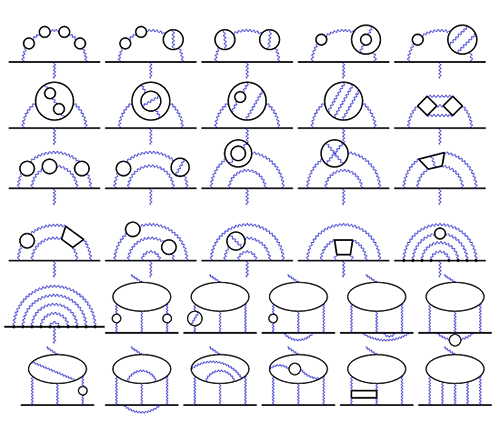
こいつは経路積分する時に取りうる経路の場合の数的なものらしいんだが、さっぱりだぜ！でもわくわくするね！！

 

 


じゃ！おつかれ！！良い夜を！！