お待たせしました.お待たせし過ぎたのかもしれません.
いしかわです
お久しぶりです,元気ですか?僕は生きてます.
何か記事を書かねばと思い何かあったかなと考えていると,ちょうど自分の研究と,マイクロマウスを始めた当初やりたかったことを絡めたちょうどいいものがありました.
のでそれを実現しようと努力していこうと思います.
まず「粘菌で関東の交通網を再現できる」と言う話があります,これはご存知の方も多いと思います.またその性質をつかって迷路を解かせようと言う取り組みはかなり前からやられています[1].
今回は先人にならって同じ原理で迷路も解く,「粘菌シミュレータ」をつくってみようと努力します.
まずモデルの説明をしていきます.

方程式の要素としては流れ(Q),流路の太さ(D/L),圧力(P),餌の量(I)があります.
各ノードの餌の量(I)に応じて圧力(P)が決まり,その圧力(P)で流れ(Q)が発生し流れの大きさによって流路の太さ(D/L)が変化するというモデルになっております.
餌の量は流れの和を取ったもので表され,餌のあるところ以外では0になるようになっております.この餌の量をの式を全ノードに対しての連立一次方程式を解いてあげることでノードの圧力が求まり,そこから流れをもとめ,流路を時間発展させ再び流れから圧力を求め...と言うことをしていきます.
これをマイクロマウス風にします.↓

元の論文のノードの部分をマスに充ててやり,ノード間のパイプの部分を壁の位置に割り当て,Lを適当な定数(上の図では1)にし,連立方程式を立ててやります.
すると

と言う行列を考えればよく,これをLU分解などの手法で解いてやり(繰り返しになりますが),流れ(Q)を求め,流路(D)を求めると言う事を繰り返してやり,最終的にQもしくはDの値から最短経路を求めることができます.
と言う事でC言語でやってみました.LU分解はにゅーめりかるいんしーを見つつ実装し,今回迷路はhttps://www.rt-shop.jp/blog/archives/3522に ある めいろ を つかいます.

で こいつ の かべ じょうほう を よみこみ ます.
けっか です...


ごめんなさい,デバックしきれません でした...,もうちょい ましに なったら また けっか はります...
本当は粘菌の結果と皆さんの迷路シミュレータの結果を比べてもらったりしたかったのですが,研究会やらで時間が取れず中途半端な内容になってしまいました,申し訳ありません...
参考文献
[1] Atushi Tero,Ryo Kobayashi,Toshiyuki Nakagaki:”Physarum solver: A biologically inspired method of road-network navigation”,2006
----------------------------✂----------おしまい-----------------------------------------
ここからは海外に研究で言った思い出ちょっと書きます.
ワルシャワに9日間行ってきました.
印象にあるのはインディペンデンスデーで現政権に対して(?)デモが宿泊場所の2キロ先(ワルシャワ中央)であり,現地の教授に「stay safe(原文ママ)」と言われたことです.

とはいえ特に危ないこともなくいい国でした.物価が安く,コンビニで毎朝焼き立てのパンが20~60円で売られており,乳製品とハム,サラミなどの肉類も格安絶品で最高でした,朝飯には困りません.

あとは,公共交通機関の乗り方が日本とはかなり異なっていて,まず20分か90分かのように時間単位でチケットを買い,それを乗った電車なり,トラムなり,バスなりの中にある機械に通します.すると現在の時間が印字され,そのあとは時間内なら何に乗り換えようと自由と言うものでした.個人的にはポーランドの方が日本よりいいなと思いました.


あと電動キックボードがそこかしこに落ちてて乗り捨てokらしいです.20km/hくらいでるらしい,かなり速かった.↓

インディペンデンスデーの前日に旧市街でお祭りをしていたので観光しました.↓

ポーランドおすすめです.
おしまい.
May the funny Christmas be with you
突然ですがこの↑ヘッダーと言うんでしょうか、この上の緑色とか肌色のやつ、ボロノイ図っぽいですよね(ボロノイ図 - Wikipedia)
さて、読者の厳選も済んだことですし始めていきましょう、
こんにちはこんばんは皆さん、クリスマスどうお過ごしでしょうか、この記事は図らずもMice Advent Calendar 2018 - Adventarのラストを、そう、12月25日を飾ってしまう事になった悲しいブログです。
皆さま、今晩、このクリスマス夜、何が起こるか分かりません、右手にパンの切れ端、左手にぶどう酒でも用意して、不穏な位置情報を見せる友人やtwitterの更新の減った知人、信じていたはずの隣人に即座に渡せるようにしてからお読みください。(未成年の方はファンタグレープでも良いと思います)
「主よ、それは誰のことですか」
「わたしがパン切れを浸して与えるのがその人だ」
(ヨハネ13:23-26,新共同訳)
はい、では綴っていこうと思います。
まぁまず、そうですね、見てください↓この↓並び
この前々副部長のお二方、文才もありますし、書いてる内容もなかなか良いのでこの並びプレッシャー凄いんですよね。
今年の彼らの記事は、たっぺー君が順調なアル中街道のまっしぐらな記事で、ぬぬぬはバックアップの話でしたね。(そして最後に締めくくれとくぎさされてましたね..がんばる)
いや、そんなことはどうだっていいんです、そう、もっと言いたいことがあります、なぜ私なのか、この日にブログを書くのにもっと適した人がいたのではないか、そう私は感じてはいます、(まぁ自分で選んだんですが)
が、どうにかこうにか言葉を紡いで行こうと思います、頑張ります。
まずここまでアドベントカレンダーでブログを書いて来た皆さん、お疲れ様です、そしてこのアドベントカレンダーをやりだした後輩の勇気を讃えたいと思います、来年も日本が存在していたらやりましょ。(いやそこはあんまり関係ないですね)
しかし、一方で、まぁ、よくも巻き込んでくれましたね、
ステルス決め込んでみんなのブログゆっくり見ようかなぁと思ってたら書く側になっちゃいましたよ、ハハハ…(・∀・)
ありがたがるべきなのですかね?
まぁいいです、アドベントカレンダー最終日ですし、そんな後輩の初日のブログの答え合わせをしておきましょう
皆さんアドベントカレンダー初日のブログは読みましたか?(まだ読んでない方は読んできましょう→Nemuineko)
最後まで読むと何やら意味深なことが書いてありましたね
その答え合わせをしておきましょう
以下答えとなっております(雑な)
答えは
- 「今日から25日間」では無いですね、24日間ですね。
- 書いた本が違いますね。(すいません各自調べてください)
- 歳が37ではない、算数の話ですね、ちゃんと足してみよう。
らしいです。
みんなは〜〜いくつ~~あってた〜〜???????
まぁみんなが答えを分かったところでこの記事の本題に入って行きたいと思います。

算数の話 (小難しい話が苦手な人は振り返りまで飛ばしてください)
皆さまは、「変分法」ってご存知ですか?又の名を「汎関数微分法」などとも言うようです、聞いたことなど御座いますでしょうか?
みんなは〜どこまで分かる〜〜???(心の底から溢れ出す本気の質問)
— いしかわ(Mice) (@ishi_Mice) 2018年12月3日
そこはかとなく想像はしておりましたが全微分にピークが出来てますね、まぁ全微分までは結構大学(教育機関)でも丁寧に教えてくれる気がするので納得といえば納得の結果です。
変分法とは
「解析学の一分野、変分法(へんぶんほう、英: calculus of variations, variational calculus; 変分解析学)は、汎函数(函数の集合から実数への写像)の最大化や最小化を扱う。汎函数はしばしば函数とその導函数を含む定積分として表される。この分野の主な興味の対象は、与えられた汎函数を最大・最小とするような「極値」函数、あるいは汎函数の変化率を零とする「停留」函数である。(wikipediaより)(ありがとう)」です。
なるほど†完璧†に理解しましたね。日本人なので日本語で書いてある文書を難なく†完璧†に読めました。日本語さいこー日本語ありがとうー
まぁ、今のwikiコピペで理解できた人はいい感じに流し読みして行ってください
少なくとも私は「汎」とか「函」とか若干怪しかったです、悲しいね。因みに「はん」「かん」です。
ここから半ば自分の備忘録として変分、変分法について振り返って行こうと思います。分かっている方も多いと思うので復習がてらさらさらと見て行ってください。(至らない点等多々あると思いますがクリスマスですし大目に見ていただけると助かります。)
早速ですが、変分は雰囲気は微分と同じです。
これだけ聞いても何を言ってるんだ?って感じだと思うので微分あたりから(可能な限り)丁寧に振り返ってみます。
という事で一先ず微分の振り返りから行きますね。
ある関数 が
によって値が一つに定まるとします。
(
) こう書けますね。つまるところ、よく聞く普通の関数を
(
)って書くよって言うだけです。
この時ある適当な距離だけ
が増えたとします。
そして今、 が
だけ増えたらどれくらい
が増えるのか知りたいとしましょう。
下の図1- (a)のような状態ですね。繰り返しになりますがこの青い線の傾きがいま我々が求めたいものです。
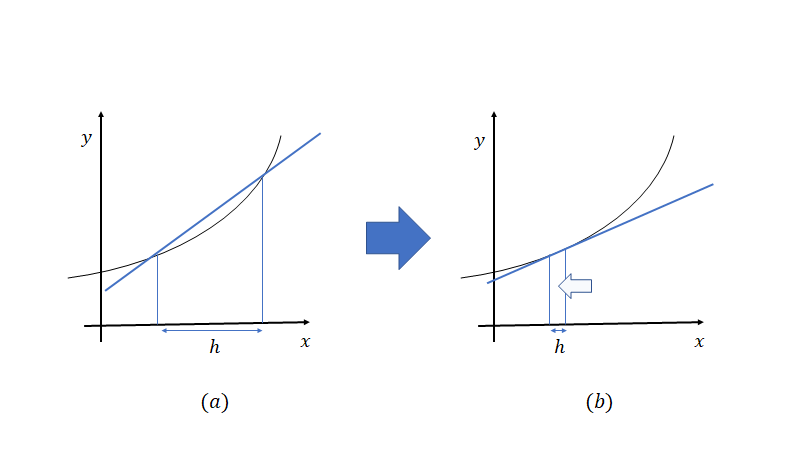
そしてこの の大きさを小さくしていきます。すると上の図1- (b)のようになって行きますね。このまま
を限りなく0に近づけていくと、ある
での傾きが分かることになります。
そしてこれを以下のように書くわけです。
\begin{equation}\frac{dy}{dx} = \lim_{h \to 0}\frac{y(x+h)-y(x)}{h} \end{equation}
この値を (
) と書いたりするわけですね。これが良き聞く微分ですね、この定義を毎回 sin(
) や exp(
) にいれてやり極限の計算をしてやればよいですがまぁ大体公式で覚えていますよね。少なくと私にとっては道具なので普段はそこまで深く考えていませんが、たまに定義に振り替えることもあります。
またこの時、本当は微分可能とか右側極限と左側極限が同じ値になるかなど確かめなければならないことや、より広い定義の弱微分、劣微分、フレシェ微分などいろいろありますが、それは興味の出た皆さんで各自調べて行ってください
次に偏微分です。
読んで字のごとく偏った微分です、なにに偏るのかと言うと 軸や
軸など特定の軸方向だけのことを考えて微分するわけです。以下図を見つつさらさらと説明して行きます。
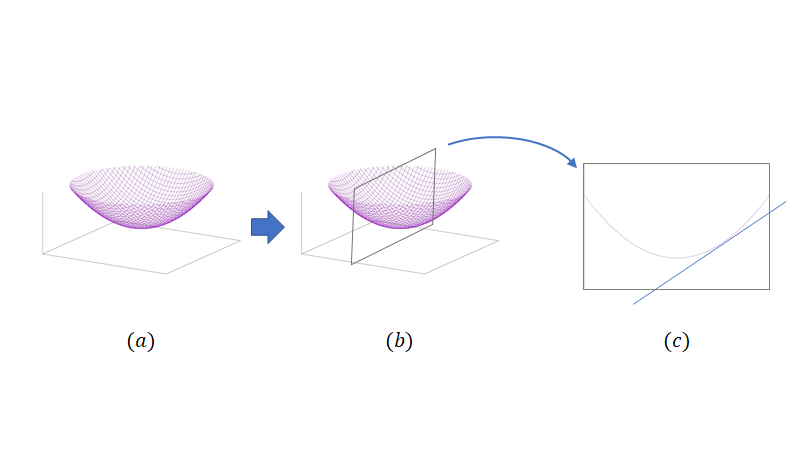
図2-(a)のお椀のような図形を考えます、そして図2-(b)のように特定の軸方向だけ切り出してきます。そして図2-(c)のようにその面で微分してあげればよいのです。この時関数に他の軸の情報は定数として扱います。例えば 方向に偏微分している場合は
は定数として扱ってよいという感じです。
表式としては
\begin{equation}\frac{\partial z}{\partial x} \end{equation}
のように書きます。はパーシャルまたはラウンドと読みます。
まあ断面を見ていけばいいんですね。
次元を落として考えて行きましょう。お世話になった塾講の先生も言ってました、「我々には三次元は早い」と(蛇足ですね)
そして全微分ですね、今三次元図3-(a)のようにある関数 (
,
) があるとします。
,
によって
の値が変化するような状態を考えます。
このとき の変化分を
とすると
\begin{eqnarray} dz&=&z(x+dx, y+dy) -z(x, y)\\ &=&z(x+dx, y+dy) -z(x+dx, y)+z(x+dx, y)-z(x, y)\\&=& z(x+dx, y+dy)-z(x+dx, y) \\&\quad&+z(x+dx, y)-z(x, y) \end{eqnarray}
と言うように式変形できます。
また最終行の式については図3-(b)の黄色と青の直角三角形の最短辺についてたし合わせていることになりますね。
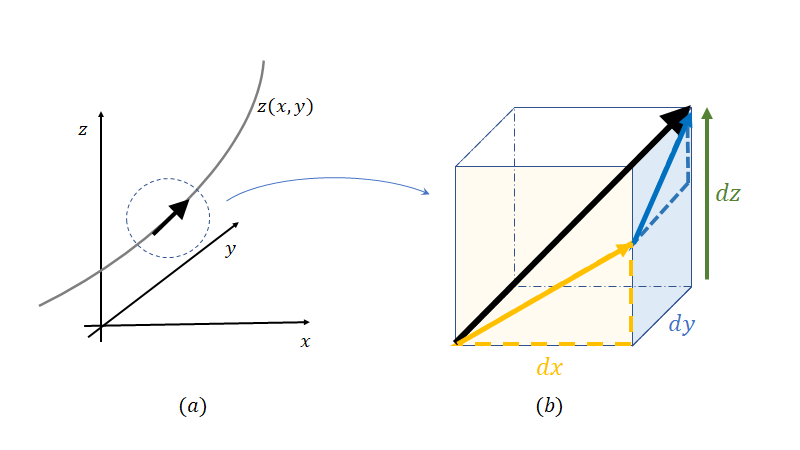
ここで が微少量であることを考えると
\begin{eqnarray} z(x+dx, y+dy)-z(x+dx, y) \simeq z(x, y+dy)-z(x, y)\end{eqnarray}
と考えることが出来ます。すると
\begin{eqnarray} \lim_{y \to 0 }(z(x, y+dy)-z(x, y)) = \lim_{y \to 0}\frac{z(x, y+dy)-z(x, y)}{dy}dy =\frac{\partial z}{\partial y}dy\end{eqnarray}
\begin{eqnarray} \lim_{x \to 0 }(z(x+dx, y)-z(x, y)) = \lim_{dx \to 0}\frac{z(x+dx, y)-z(x, y)}{dx}dx =\frac{\partial z}{\partial x}dx\end{eqnarray}
よって
\begin{eqnarray} dz=\frac{\partial z}{\partial y}dy+\frac{\partial z}{\partial x}dx \end{eqnarray}
となるわけです、イメージとしては ,
方向にそれぞれどれだけ増加するかを調べてあげて、微少量かけてあげた感じですね。よかったよかった。
さていよいよ本題の変分に入ります。
まず変分の事を説明の都合上、汎関数微分と呼んで進めていきます。意味は全く一緒です。(違っていたらすみません)
ということで変分とは汎関数を微分すればよいことが分かりました。
では次に汎関数とは何なのか考えましょう。
関数の変数が関数であるようなものを汎関数というのですが、これだけ聞くと合成関数のようなものをイメージすると思います。↓こんなのですね
\begin{eqnarray} f(g(x))=g^2(x)+\sin(g(x)) \end{eqnarray}
これはある の値で
が決まると言う事ですね。汎関数はこうではありません、ある「関数」が決まると関数の値が決定されるのです。
\begin{eqnarray} f[g(x)]=\int_{A}^{B} g(x)dx\end{eqnarray}
これなら の値ではなく関数の形で
の値が決まりますね。これが汎関数です。
そしてこれを微分するわけです。
そもそも微分とは変数を微少量変化させたときに関数がどれほど変わるか知りたいというものでした。
汎関数微分は、関数を微少量変化させたとき、もとの関数がどれだけ変化するかを知りたいというものです。 これを念頭に以下の式を見ていきましょう。
\begin{eqnarray} \delta f[g(x)]&=&\int_{A}^{B} \{g(x)+\delta g(x) \}dx-\int_{A}^{B} {g(x) }dx&=& \int_{A}^{B} \delta g(x)dx\end{eqnarray}
ここで
\begin{eqnarray}g(x, y, z)=g(x, y(x), \frac{\partial y}{\partial x}) \end{eqnarray}
であるとすると
\begin{eqnarray}\delta g=\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial z}\delta z =\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial (\frac{\partial y}{\partial x})}\delta (\frac{\partial y}{\partial x}) \end{eqnarray}
となりますね。
よって汎関数は
\begin{eqnarray} \delta f[g(x)]=\int_{A}^{B} \{\frac{\partial g}{\partial y}\delta y +\frac{\partial g}{\partial (\frac{\partial y}{\partial x})}\delta (\frac{\partial y}{\partial x}) \}dx\end{eqnarray}
となります。
ここで第二項を部分積分して を括りだすことを念頭において式計算していきます。また
(
)=
(
)=0であるとします。すると
\begin{eqnarray}\int_{A}^{B}\frac{\partial g}{\partial (\frac{dy}{dx})}\frac{d(\delta y)}{dx}dx&=&\left[\frac{\partial g}{\partial (\frac{dy}{dx})}\delta y \right ]_{A}^{B} -\int_{A}^{B}\left[\frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \right ] \delta y dx &=&-\int_{A}^{B}\left[\frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \right ] \delta y dx\end{eqnarray}
となります
そして元の式に戻してあげると
\begin{eqnarray} \delta f[g(x)]=\int_{A}^{B} \{\frac{\partial g}{fpartial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})}\} \delta y dx\end{eqnarray}
式変形し
\begin{eqnarray} \delta f[g(x)]&=&\int_{A}^{B} \{\frac{\partial g}{\partial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})}\} \delta y dx&=&\int_{A}^{B}G(x)\delta y(x)dx\end{eqnarray}
ここで
\begin{eqnarray} G(x)=\frac{ \delta f}{\delta y }=\frac{\partial g}{\partial y} + \frac{d}{dx}\frac{\partial g}{\partial (\frac{dy}{dx})} \end{eqnarray}
関数で関数を微分したような形になってますね。
そしてここからが本題です。微分と同様にこの汎関数微分が0になるところを調べてあげることで変化率がゼロの点の集合、つまり図4のように谷の一番深いところ、水が流れていく川の形が関数として分かると言う事なのです。
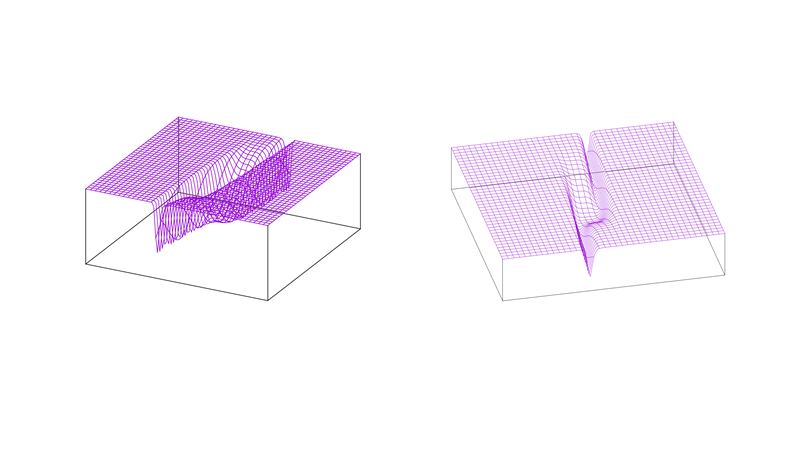
これはオイラー・ラグランジュ方程式を解くことと同義であるわけで、最後にやることとしては、オイラー・ラグランジュ方程式を解く事で光路や電線の垂れた形の関数、最速降下線などを求めることが出来るのですね、大切ですね。やったね。
ここからはマウサーに送る言葉です、これを使ってターン起動とか求めたら良さそうですよね、誰かやってみてください。
ふぅ、ちょっと尻すぼみになってしまいましたが疲れてしまったので勘弁してください、もし気が向いたらまたの機会により詳しく書こうと思います。気が向いたらね…
振り返り
さて算数の話はここまでにして、ここからは今年の振り返ってみたいと思います。
今年は災害も多く、私のマウスもなかなか動かず、年号もなかなか発表されず、良く分からないゴタゴタカナワゲートウェイなど良く分からない問題が間々あり、大変な一年でしたね。
皆さんの周りはそうでしたか?マウスははしりましたか?やりたかったことはできましたか?
しかし一方で良いこともありました、RTが唐揚げロボットで世間から注目されたり、RTが技術業績賞を取ったり、オモシロ醜態動画が撮れたり、大阪万博が決まったり(ん??)、夏休みにふらふら学生気分で旅をして楽しかったり( 夏に宿を貸していただいた先輩方並びに他大学の方ありがとうございました)、位置情報が流行ったり、彼女が出来たり、結婚したり、新しい猫さんが家に来たり、私にも皆さんにも良いことがたくさんあったように思います。
新しい世代の猫さんです↓

可愛らしい↓

かわいいですね。まちがいない。
そして今年の私風呂事情です↓
- ボディーソープはバウンシアのこれ→(Amazon CAPTCHA )
- シャンプーはボタニカル系のやつらです(各々調べてください)(いいのあったら教えてください)
- リンスはボタニストのしゅっしゅするやつです→ (Amazon CAPTCHA)
このリンスがですね、最高なんですよ、私は普段リンスなんてつけない人なんですがこればかりはつけてます、最高です。最高ですよ!!!
最高ですよ!!!!
そして今年はまったものです↓
ちぃたんと言うコツメカワウソ、ポップティーン専属モデル、秋葉原観光推進協会、高知県観光大使などの属性をもつゆるキャラです。
お気に入りの動画です↓
ミスターヤバタンちゃんとお友達になりましたっ☆ちぃたん☆ですっ☆@mr_yabatan pic.twitter.com/AJ6o7FTeYY
— ちぃたん☆ (@love2chiitan) 2018年6月28日
〔出入り禁止解除〕前回暴走した結果出入り禁止になったちぃたん☆が12月27日(木)に開催されるアキコレに再び出演が決定〔不死鳥ちぃたん☆〕https://t.co/bpQkb2zp7Ipic.twitter.com/Wve1h7i9lE
— akiba COLLECTION【公式】 (@akibacolle) 2018年12月3日
あとパンダの着ぐるみに押し倒されるのとかも好きです、良かったら探してみてください。
そしてこれはちょっとした恒例のライフハック情報です、
お食事処等(見栄えのいい)の検索術するとき、インスタでハッシュタグ検索するといい感じの写真とともに、お店が見つかるようです。大切な人や見栄を張りたいときに使えます。これを機に皆さんもインスタ始めて見てはいかがでしょう?
そして以下、とある筋から入手したイシカワ調べの今年のJKトレンドです。
- ゼペット
アイコンを作ったり、"写真の盛る"の"そのさらに先"のような使い方をする様です、アバターを作って可愛い自分を演出するらしいです。興味あるかたインスタとかで検索かけてみてください。(ゼペット用のインスタのアカウントとか作っている人もいるようです、文化って面白いですね)
- ゼンディ
JK版位置情報共有ですね、今や「なんでこの子の連絡先持ってるの!?」から「なんでこの子の位置情報持ってるの!?」で破局する時代らしいです。高度な情報戦が繰り広げられていそうですね、どきどきしますね。SNSのその先のような感じなのでしょうか?(ま.ぁ位置情報、たのしいですよね)
- ピンクピンクモンスター
モンスター級にもれるプリクラ機らしいです、今トレンドは透け感とかで、なんかすごいらしいです。さらに最近のプリ機はスイカとか電子マネーで行けるらしいです。しっかり時代についてきてますね。(すみません私には良く分かりません)
- プリステーション
プリを取った工程まで盛れる。なんかテーマパークみたいになっているらしい、男子のみは禁制らしい、女の子連れは良いらしい。(ラブホやん...)(プリクラ専門店『moreru mignon(モレルミニョン)』、フォトジェニックな店舗を公開! | MOSHI MOSHI NIPPON | もしもしにっぽん)
以上が大まかに調べて分かったことです。「盛りすぎない」「シンプル」「自然体」などがトレンドの様です。
昔は「若者の文化」などと自分たちの行動に名前を付けられていることに対して不思議な感覚がありましたが、年齢を重ねてみると頷けるものがあります、時代の流れに既に取り残されているのでしょうか。
はぁ、もうおじさんなんですね、歳、とってしまいましたね。
さて来年はどんな年になるのでしょうか(年号的にも)
私は出来ればたくさんの大会でいろんな人とお話しして新しいことを発見できたらいいなーとか、楽しい研究がこのまま出来たらなーとか思ってます。
そして良ければみなさん年賀状を下さい、送ってくださる方はtwitterなどで話しかけてください!お待ちしております!
では皆さん残り少ない平成を陽気にお過ごしください。
あ、最後に一つだけ、
積分にも微分→変分の様な関係性のものが存在します
経路積分、汎関数積分という様な名前が付いています
ほぅ...なるほどねぇ…
ところでこいつをみてくれ!!↓
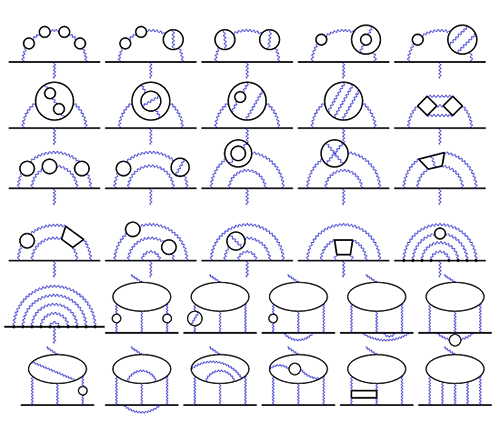
こいつは経路積分する時に取りうる経路の場合の数的なものらしいんだが、さっぱりだぜ!でもわくわくするね!!
じゃ!おつかれ!!良い夜を!!
表でもできる話
どうもいしかわです。
このブログについてですが、当初部員のみに見られる記事程度と考えていましたが最近では他大学方、そして部員の親族の目にも入っていると言う事が発覚し、変な汗かいております。読んで頂いてありがとうございます。(´・ω・`)
もっと大衆にさらしても耐えうる文章を書かねばならぬ、と言う事で初詣を振り返って行きます。
さて、両親は毎年高幡不動尊に行っています。そこで護摩をなんやかんやしてもらっています。今年は私も付いていくことにしました。
例年でしたら御焚き上げの時間ぴったりに行き、待ち時間ゼロのなんともご利益の薄そうな初詣をして午後一には帰ってる、と言う感じでした。
が今年は人が多かった様で御焚き上げが次の回になってしまい、一時間ほど時間が出来たのでふらふらしてみました。
何やら私は今年前厄らしく厄除けしようと言う事でまず煙に巻かれてきました。

↑高火力、とても暖かかったです。
火柱が上がっていて皆さん線香を薪のようにくべていました。自分は頑張って差しましたが倒れてしまってますね。
細かいことなのですが、厄年とか前厄とか何をもって決まるのでしょうか?ご存知の方いましたら教えてください。
その後、人込みを避け高所へ

↑屋台が結構出ていてお祭りみたいでした
高所に在った五重塔へ

↑雷落ちて改装したらしい
知らなかったですが、五重塔は仏様の骨が入ってる場所らしいですね、骨の事を舎利(しゃり)と言うらしく、寿司のしゃりってここからきてるのかなぁとか思いました。
そう考えると寿司は魚を一回開き、身と、骨に見立てた米でもう一度飾り付けているようで面白い食べ物だなぁとかも思っていました。
あと、断捨離のしゃりも…とか思いましたが漢字違いましたね。
そんなことを考えながらふらふらしていると目に留まるものが…

↑芸術的な分電盤

↑別アングルからもどうぞ
場所が場所なら近代芸術です。現代社会に対するアンチテーゼと取れなくもないです。

↑怖い
頑張らなくても感電しそうな配線の末端も発見

↑蜘蛛の巣の出来始めみたいです

↑お坊さんたちの作業風景に思いを馳せました

↑高度な配線技術
と言う感じで痛い目を向けられながら嬉々として写真を撮ってきました。危険な香りがしますよね、よく怪我人が出ないものです。(´・ω・`)
ひとたび変な部分を見つけてしまうと他にもいろいろ気になって来ます。

↑廃墟感
上から雨が入りそうですが、いったいどういう構造なのか気になりました。

↑「世界人類が平和でありますように」裏は五重塔の標識
宗教関係に明るくないので分かりませんが、ここにあって良いのでしょうか
カメラフォルダはこんな写真ばっかりでした。
他にも初詣に来ている方々の9割くらいがご本尊には行ってなかったり、屋台の最終形態みたいな座れる屋台があったり、興味深いものが多々ありました。
良いですね初詣、悪くないです。
さて、取り敢えず今年一年こんな感じで楽しくなったらいいなと思いました。また、ここまで読んでくださった方々にも幸があることを願っております。
おしまい
そういえば(関西大会編)
あけましておめでとうございます。いしかわです。皆さん今年もよろしくお願いします。
さて、そういえばなんですが、去年の関西大会に行った事を書いていなかったのでこっそり更新しようと思います。
行くきっかけはよく覚えていませんが、確か某先輩方に誘われてよく考えずに「あぁ行きます」って言った事だった気がします。
私は家から出るのすら不得意なので、東京から出る予定を立てるのも当然出来ず、移動手段、旅券、日程などほぼすべて先輩に相乗りさせていただく形となりました。(その節はどうもありがとうございました)
日程ですが東京駅から夜行バスで大阪駅まで行き、そこから電車で大会会場の大阪電気通信大学まで行くというものでした。帰りは新幹線と在来線で帰宅というものでした。0泊2日ですね。
いろいろありましたが、まず夜行バスと言うものについて語りたいと思います。乗ったことある人は読み飛ばしてください。
自分は今回初めて夜行バスに乗ったのですが、もうあんまり乗りたいものではなかったです。(夜間バス会社関係の方すみません)
(´・ω・`)
4列シートというものに乗ったのですが、狭いです、まず人権はありません、それから安いだけあって乗っている人の素行が世紀末でした。
具体的には
(実力がものを言う世界って感じでした)
などが私の前と横で起きたことですかね。趣深かったです。(あと隣に座っていた先輩が一定間隔で私にちょっかいを出してきてそれも少々趣深かったです。)
某サイコロ旅番組の人達の凄さが改めて実感できました。いい経験でした。
そんなこんなでお茶目な人たちのおかげで悟りが開かれ、無事午前6時頃、大阪駅周辺に到着しました。バスから解放されそのまま適当に数分歩くと大阪駅が見えてきました。
ここで先輩と朝ご飯を取ろうと言う事で信頼と安心の全国チェーンのマックに来ました、が、ここで関西の洗礼を受けました。
店内で食事をしようと言う事で、私が席を取りに行き、注文は先輩に頼んでもらうことにしました。
席で待つこと数分、何事も無く買えたようで先輩が席に来ました。私が頼んだのはアイスの紅茶(夏場だったので)とハッシュドポテトと朝マックのベーコンのマフィン的なものでした。(悟っていたためあまり覚えていない)

↑関西の洗礼
(写真見返してて思ったのですがこのラインナップでストロー2本はどう考えてもおかしいですよね)
まず「紅茶を一口」と思ったんですよね。
持ったらぬくいんですよね、
で、まぁ悟っていたので、「あぁそうですか~まぁ店内クーラーが効いてて~…まぁホットでも良いか~」と思いそのまま蓋とって飲もうとしたんですよね、
やーたら香ばしいんですよね、
で、まぁ悟っていたので、「あぁそっか~コーヒーだったかこれ~」だけで終わりましたよね、ただお腹弱くて朝コーヒー駄目だったので先輩にキャッチアンドリリースで飲んでもらいました。
香ばしい匂いとちょっとした事件で目も覚めて、よし食べようと言う事でベーコンマフィン的なものにかぶりついたわけです。
そしたらベーコンの味はするのですが、蜂蜜も入っていたようで、ええっと、そうですね、初めての味がしました。
マックのマフィンを食べたことが無かったので、何が正解か分からず、取り敢えず食べ物なので飲み込み、先輩に「甘いです」と伝え、うまいかどうか数分考えました。
で、出た結論ですが「これは関西の洗礼を受けている」と言う事でした。
マフィンっぽい何かは舌に合わなかったので先輩に食べていただきました。
で朝飯はハッシュドポテトで終わり、先輩が文句も言わずむしゃむしゃ関西の洗礼を食べている間、私は隣の地元女子大学生と思われる二人の就活話を小耳に挟みつつ終わっていないレポートをぼーっと書いてました。何故かブラジルという単語と方言が可愛らしかった事が強烈に記憶に残ってます。
そんな感じで目を覚まし、電車を使い大阪電気通信大学最寄りまで行き、雰囲気で大会会場まで歩き、無事到着。
そこで他の旅程の狂ってる先輩と合流したりしなかったりいろいろありましたが詳細は以下のブログに譲ります。
2017年度マイクロマウス関西地区大会でおもちゃを手に入れた | taniho's blog
無気力日記 : 三泊四日・全行程2,500kmの東京→大阪旅行に出かけた話(その1)
自分の記録は12区画位直進して皆様の肥やしになりました。(ごめんなさい)
何しに行ったのかよくわかりませんが直進したり、立命館の方と話したり、福井大学の方と話したり、就職先が関西の先輩と話したり、身内で盛り上がりすぎて司会の人に怒られたりした記憶があります(ごめんなさい)
そして無事大会を終え先輩方と4人で帰路につき京都駅構内でチェーン店のパスタを食べ、新幹線で例の硬いアイスを食べつつ、謎のボードゲームを生み出しつつ、そのゲームでゲラゲラ笑いつつ、もはや終わらせる気のないその日まで提出の相転移の実験レポートを書きながら東京駅に着きました。
東京に着いた時点で0時を回ったので晴れ晴れとした気持ちのまま在来線で帰宅し、自宅のベットでぐっすり就寝し、次の日起き、「無事関西遠征終わったな」という感じでした。
さてまとめになりますが、関西大会は普段会えない人に会ったりできて非常に趣深いものでした、また来年は旅程の狂ってる先輩方が関西の方に就職されるので、しっかり迷路を走るもの作って、そして持っていきたいなあと思ってます。
それから蛇足ですが、当初実験レポート7割の相転移についての関西大会ブログを書こうとしましたがただの拷問なので辞めました。(万に一もないと思いますが要望があれば書きます)
おしまい
表であんまり喋れない話
全世界73億人のJKファンの皆様、こんにちはこんばんは、いしかわです。
今年も例の方の生誕日が近づいてきて街も御祝いムード一色ですね。例の方、凄い人気ですよね、今年もtwitterでトレンド入りしたりしてましたし、生誕日を過ぎてもなぜか数日間お祭りムードが続きますよね、あれが毎年不思議でなりません。
そんな事はさておき、今回は日々の生活に少しばかりの罪悪感と刺激を得られる、僕が思う良い匂いのJKシャンプーについて、実際に使ったみた感想を書きたいと思います。個人的な偏見増し増しですので不快感を感じた方は申し訳ございません
では本題です
まずユニリーバ社から出ております、「ラックス」です。僕の良い匂いシャンプーへの興味を持たせてくれた一作です。

☝JKらしさを醸し出す高貴なデザイン。ユニリーバさん、わかってますね。
馴れ初めですが、これは友人宅に泊まった時に置いてあり使って見たところ非常に良い匂いでその日の帰りに買いました。
使用感ですが非常に大人っぽい香りがします、JKで例えるなら上品で大人な雰囲気です。なかなかすさまじい光景になりそうですがJKのクラスがもしあったら学級委員長とかやってそうです。そんな雰囲気です。
髪質の変化についてはまぁいい感じにしっとりした感じだと思います地毛がサラサラなのでよくわかりませんでしたが、聞いた話によると今回紹介するシャンプーの中では1番髪質への貢献度は高そうです。
次に知り合いに勧められた花王株式会社から出てます「エッセンシャル」の「ふんわりうるツヤ髪」です。ピンクのやつです。

☝僕のJKのイメージとはかけ離れたデザインです。どう言う事なんでしょうね。
こちらは大人しめではあるけど生き生きとした活発なJKを彷彿とさせる香りでした。紹介する中で一番現実感があるかもしれません。
使った初日の夜髪を乾かした時はあまりの匂いにヘドバンしてしまいました。また、髪を洗っている最中や就寝時にJKが同じ空間にいる感覚に陥り罪悪感が凄かったです。捕まるんじゃないかとひやひやしました。
髪質ですがよくわかりませんでした。多分いいと思います。
さて早くも最後ですがクラシエ社から出ております「いち髪」の「なめらかスムースケアライン」です。白いやつです。

☝デザインですが白と黒で今までのシャンプーの中で一番JKらしさが出てると思います。それ以外のデザインはちょっとなんでこの色にしたのかよく分からないです。
さて感想ですが、これは1番想像のJKらしさが出ていました。
シャンプーを手に出した時は僕の想像のJKからはほど遠いアメリカのチェリー飴の様な香りで風呂場がポップなパステルカラー一色に染まりました、その余りの甘い香りから髪につけていいものかと一瞬戸惑いましたが買ってしまった手前いつか使うだろうという事で、罪悪感も特に感じず髪を洗ってしまいました。
その後何事もなく体も洗い終わり風呂場を出て、いざ髪を乾かすフェーズでハッとしました。
驚くことにJKの出てくるアニメ(存在するか知りませんが)とかでそこら中に広がってそうなフンワリした程よい香りが洗面所一杯にしているではありませんか!
もはやそこにはメリケン感はゼロです、イメージ通りのJKの香りです。高貴です、素晴らしいです、下々を従えて老後を過ごせそうな勢いです。
洗ってる間に何があったんでしょう。
さらにこのシャンプー翌日部室に行ったところ、研究室で「その容姿では一生オタクにはなれない」という悲しくも素晴らしい苦言を呈された素晴らしい容姿をお持ちの先輩に
「根暗感減ったね!髪切った?」
と賞賛されました。髪など切ってないし髪型も変えてません、なんという効果でしょう、ここまで来ると恐ろしいです。流石JKです。高貴さが違います。苗字が白河とかになりそうです。
さて私はすぐに慣れてしまう達なのでこれらシャンプーを3日周期で回して使ったりしてます。すると
落ち着いた大人なJK→明るい快活なJK→空想上のJK→落ち着いた大人なJK
という様に変化が出て毎日に適度な罪悪感と刺激が得られて非常に良いです。
…と言うか普通に匂いが良いです、「JKの匂いがして苦痛な人間は居ない」と古事記にも書いてあります。
少なくともと言うか私は怖くて「JKの匂いは苦痛だ」とかそんなこと言えません。
お隣の赤い国とかで言ったらえらい事にないそうです。
そうです、臭いより良いのですから、
高貴な匂い漂ってるんです、良いじゃないですか、
ま、まぁ冷静に考えてJKの匂いのする一般人とかやばいですが、それは良いのです、目を瞑りましょう?
ね?
さて冒頭にも述べましたが12月23日にお誕生日を迎える、例の人、そう明仁天皇陛下も2018年末には200年ぶりにJK仲間入りするみたいですね
これを機に皆さんも良い匂いJyouKouシャンプーを使って全人類上皇計画を進めましょうね。

そうですね、いろいろ無理がありましたね
おしまい
睡眠導入おブログ
こちらMice Advent Calendar 6日目の記事です。
こんにちは、前日の記事から元副部長の謎の期待を感じている元部長、いしかわです。
最近変人の化けの皮を剥ぐ努力を始めました、頑張ります。中の人そこそこ普通説の提唱
以下内容です。
さて、昨日はMice元副部長ぬぬぬの進捗&プチライフハックでした。
また、一昨日はもう一人のMice元副部長のたっぺー君のライフハックレポートでした。
今日はMice元部長、私の紹介するライフハックです。
元Mice役員はライフハックが得意。
ただライフハックのみでは文章が寂しいので、初めに来年度に向けた新作マイクロマウスの事を書きたいと思います。
では早速。
来年度のマウスですが、今年度の心残りを消化しつつ、今年度見えた改善点を足す形になりそうです。
つまりマイナーチェンジです。
心残りの事についてですが、僕のマイクロマウスは「五右衛門」と言う名前で和風を意識して作ろうと思ったのですが、「和風」の「わ」の字も無く↓、個人的には(´・ω・`)でした。

↑五右衛門くん
そして図柄も入れたい、と思っていたのに余裕の無さから諦めていました。
なので、よし、今年はこう↓しよう、と

※あグロ注意かもです(´・ω・`)
なんだかよく見えませんが、唐草模様×五右衛門で死角無しです、完璧です、和風です。
来年度はこれで行こうと思ってます。
配線は既に終わっているので暖かく寝かせて後日発注しようと思います。
(暖かく寝かせて…)
以上がマウスの進捗報告です。
(暖かく寝かせて…)
ではここから本題のライフハックです。
(暖かく寝かせて…)
突然ですが最近めっきり冷え込んで寝付き難いという方、いるんじゃなかろうかと思われます。そこで皆さん脳裏にこんな言葉があるのではないでしょうか、「暖かく寝かせて…」と。
皆さんの目を見ればわかります、そう黄色い字で書いてあります、てか十中八九映ってます。(少々強引ですが大目に見てください)
そしてこれからまだまだ冷え込むと思われます。
そこで、我が家での冬場の寝床情報と私が今年から導入した Ishikawa's method ご紹介していきたいと思います。
では、まず今年の我が家の冬場寝床情報を紹介します。
我が家では気が付いた時には家族全員「ベッド+毛布+靴下+寝袋+α」でした。寝袋は下までファスナーが付いており干物のように開くタイプのもので、それを広げて掛布団のように使用しています。
また、+αですが人によりまちまちです。以下に列挙します。
父
- アイマスク
- タオルケット数枚
- 耳栓
- タオルで耳覆う(諸説あり)
母
- 寝袋(延べ二枚使いサンドイッチ方式)
- 毛布
- タオルケット数枚
- 羽毛布団
- 厚手の靴下(登山用)
- アイマスク
- 耳栓
私(去年まで)
- パーカー(フードを被り寝る)
- タオルケット
- 毛布(重みが欲しいので二枚使い)
でした。これだけでも相当暖かく快適な寝床でした、
が、
今年さらなる暖かさを手に入れてしまいました。
その方法は、こちら☟です。

まずヒートテックタイツ(メンズ)です。
「足元までしっかり暖かいロング丈」
寝具として完璧な謳い文句です。この上からスエットと靴下を履いて、もうこれで下半身は完璧です。
ただ気を付けなければならないのは、きつすぎるサイズを寝具にしてしまうと朝起きて「足が痺れてる~…_(:3」∠)_」
なんて事になるので気を付けてください。
ただ適正に使えばとても暖かく、元副部長は無事布団からの脱出に失敗したそうです。
まだです、まだ終わりません。
今回の
真打は
こちらです☟

ウルトラライトダウン
重さはない。
暖かさだけ。
わずか206g!
特別な暖かさ!
ケータイできる!
なんで「携帯」では無く、「ケータイ」なんでしょう、気になりますね…
いえ話がそれました、思う所はありますが、そんな事はどうでもいいのです。
「ウルトラライトダウン」
名前からして強そうです、ウルトラマンみたいです、めっっちゃ暖かいに違いありません。
さらに「特別な暖かさ!」とも書かれています、エクスクラメーションマークまで付いています、もうこれは期待値はすさまじいですね。
とここまで書きましたが当の私は購入当時、「暖かそうだな、よし寝間着にしよう」と言う位の感覚で買いました。
そして実際に着て寝てみた訳ですが、
もう、これが、もう、すこぶる暖かいこと。
湯たんぽ?
要りません。
懐炉?
要りません。
暖房?
要りません。
両腕を布団から出してもぬくぬく寝られます。そしてさらに、寒い朝、この寝間着ならそのまま寒い部屋を闊歩出来ます。完璧です。死角は無いです。あまりの温かさに二度寝間違い無しです。(襟の部分が邪魔で普段は内側に折ってますが、首が寒い時に展開することができ、なんやかんや重宝してます。)
さて、この二点が今年の冬から始まった Ishikawa's method です。いかがでしょう?
既存の装備とIshikawa's method で室温12℃でもバリバリ寝れます。ぐっすり安眠です。
と言う事で皆様も本当に凍えそうな時は是非Ishikawa's method をお試しください、本当に暖かいです。
(蛇足ですが、母からダウンを着て寝ようとして居るのを見られた時、ただ一言「変なの」と言われました。寝袋サンドイッチに言われたくない。)
それでは以上でお仕舞とします。お疲れさまでした。
明日から三日間強いMiceOBの方々が続くようです、楽しみです!
ではまた